Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- BFS
- Kotlin
- ios
- 알고리즘 공부
- 안드로이드 공부
- error
- 파이썬
- 알고리즘
- 공부
- Python
- Android
- 앱개발
- Autolayout
- dfs
- UIKit
- 파이썬 풀이
- iOS개발
- Swift공부
- 프로그래머스
- 백준 온라인 저지
- SwiftUI
- 백준온라인저지
- Til
- greedy algorithm
- 오토레이아웃
- 정렬
- 그리디 알고리즘
- Algorithm
- swift
- Clean Architecture
Archives
- Today
- Total
Tori의 개발 공부
[python구현] 정렬 알고리즘 - 선택, 삽입, 버블, 병합, 퀵 정렬 본문
정렬
선택 정렬
선택 정렬 알고리즘
- 주어진 리스트 중에 최솟값을 찾는다.
- 찾은 값을 맨 앞에 위치한 값과 교체한다.
- 정렬된 앞부분을 제외한 리스트를 같은 방법으로 교체한다.
선택 정렬 파이썬 구현
def selectionSort(x) :
length = len(x)
for i in range(length-1) :
minIndex = i
for j in range(i+1,length) :
if x[minIndex] >x[j] :
minIndex = j
x[i], x[minIndex] = x[minIndex], x[i]
return x선택 정렬 시간 복잡도
- 모든 인덱스 접근 루프문(i for문) : O(n)
- 최솟값 찾기 루프문 (j for문) : O(n)
- 총 O(n^2)
버블 정렬
버블 정렬 알고리즘
인접한 두 요소를 검사하여 정렬하는 방법
- 가장 앞 두요소를 비교하여 조건에 만족하는 요소를 뒤로 보낸다.
- 한 칸씩 이동하여 같은 방법으로 비교, 정렬한다.
- 한 바퀴 돌았을 때 리스트 중 가장 조건에 만족하는(예를 들어 가장 큰 요소) 요소가 가장 뒤로 가게 된다.
버블 정렬 파이썬 구현
def bubbleSort(x):
length = len(x)-1
for i in range(length):
for j in range(length-i):
if x[j] > x[j+1]:
x[j], x[j+1] = x[j+1], x[j]
return x버블 정렬 시간 복잡도
- 순회 루프 문(i for문) : O(n)
- 자리 교환 루프문 (j for문) : O(n)
- 총 O(n^2)
삽입 정렬
삽입 정렬 알고리즘
자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘
- 두 번째 인덱스부터 시작
- 해당 인덱스 앞쪽의 자료들(앞은 이미 정렬된 리스트)과 비교하여 삽입할 위치 지정
- (정렬 기준을 만족하다가 다음 자료에서 정렬 조건을 위배하는 순간이 삽입할 위치임)
- 삽입할 위치를 찾으면 삽입을 위해 자료를 한 칸씩 이동시킨 후 삽입
- 인덱스 한 칸씩 이동하며 같은 방법으로 정렬
삽입 정렬 파이썬 구현
def insert_sort(x):
for i in range(1, len(x)):
j = i - 1
key = x[i]
while x[j] > key and j >= 0:
x[j+1] = x[j]
j = j - 1
x[j+1] = key
return x삽입 정렬 시간 복잡도
최악의 경우는 앞의 요소들과 비교할 때 가장 앞의 요소까지 비교하는 경우이다.
- 1번째 비교의 경우 앞에 1개의 요소뿐이므로 1번 비교
- 2번째 비교는 앞에 2개 요소이므로 2번 비교...
- 총 n개의 데이터가 있을 때 1+2+3+... + (n-1) = n(n-1) / 2번 비교하므로
- 총 O(n^2)
병합 정렬
병합 정렬 알고리즘
분할 정복 알고리즘 중 하나
분할 정복(divide and conquer) 방법이란?
문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 방법이다.
즉 병합 정렬이란?
하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
- 리스트를 반으로 분할한다.
- 부분 리스트에 대해 정렬을 시도하는데 부분 리스트가 충분히 작지 않으면 다시 반으로 분할한다.
- 부분 리스트들이 더 이상 분할할 수 없을 때 정렬을 시도한다.
- 정렬된 부분 리스트들을 하나의 배열에 합병한다.
- 모든 분할 리스트를 합치도록 반복한다.
병합 정렬 파이썬 구현
def merge(left, right):
result = []
while len(left) > 0 or len(right) > 0: #left, right 둘 중 하나라도 요소 존재한다면
if len(left) > 0 and len(right) > 0: #둘 다 요소가 존재한다면
# 두 리스트의 값을 비교해서 더 작은 값 result에 추가 후 기존 리스트에서 삭제
if left[0] <= right[0]:
result.append(left[0])
left = left[1:]
else:
result.append(right[0])
right = right[1:]
elif len(left) > 0: # left만 존재한다면
#left 첫번째 값 result저장 후 기존 left에서 삭제
result.append(left[0])
left = left[1:]
elif len(right) > 0: #right만 존재한다면
#right 첫 번째 값 result 저장 후 기존 right에서 삭제
result.append(right[0])
right = right[1:]
return result
def merge_sort(list):
if len(list) <= 1:
return list
mid = len(list) // 2
leftList = list[:mid] #left 리스트
rightList = list[mid:] #right 리스트
leftList = merge_sort(leftList)
rightList = merge_sort(rightList)
return merge(leftList, rightList)병합 정렬 시간 복잡도
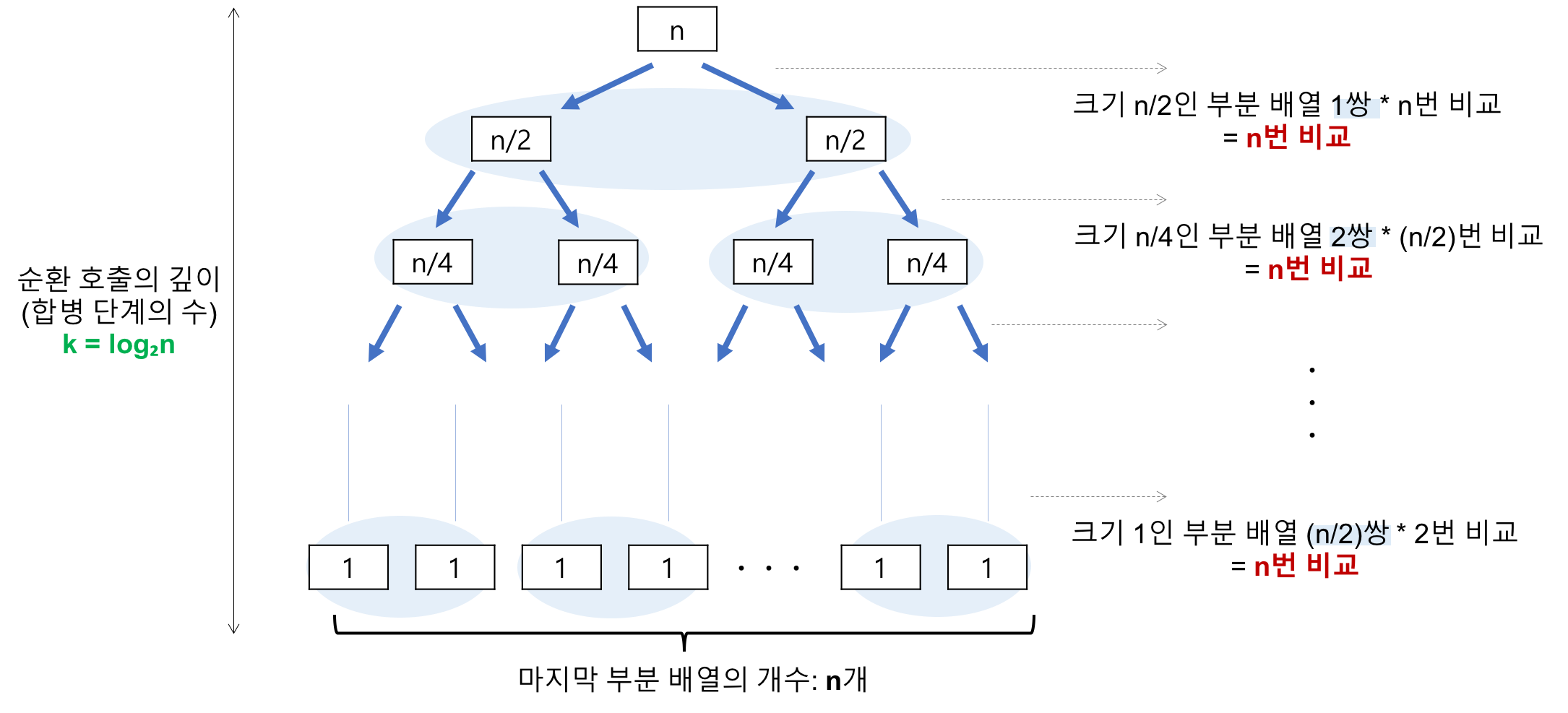
이미지 출처 : Heee's Development Blog(https://gmlwjd9405.github.io/)
- 각 단계에서 합병을 위한 비교 : O(n)
- 단계의 수(순환 호출의 깊이) : 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3 임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n) 임을 알 수 있다. 따라서 O(log₂n)
- 총 O(nlog₂n)
퀵 정렬
퀵 정렬 알고리즘
피벗을 기준으로 한 정렬 알고리즘
- 피벗을 기준으로 피벗보다 작은 요소는 피벗의 왼쪽으로, 큰 요소들은 오른쪽으로 옮겨진다.
- 피벗을 제외한 왼쪽, 오른쪽 요소들을 각각 같은 방법으로 정렬한다.
- 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
퀵 정렬 파이썬 구현
def quick_sort(array, start, end):
if start >= end: # 원소가 1개인 경우 종료
return
pivot = start # 피벗은 첫 번째 원소
left = start + 1
right = end
while(left <= right):
# 피벗보다 큰 데이터를 찾을 때까지 반복
while(left <= end and array[left] <= array[pivot]):
left += 1
# 피벗보다 작은 데이터를 찾을 때까지 반복
while(right > start and array[right] >= array[pivot]):
right -= 1
if(left > right): # 엇갈렸다면 작은 데이터와 피벗을 교체
array[right], array[pivot] = array[pivot], array[right]
else: # 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
array[left], array[right] = array[right], array[left]
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
quick_sort(array, start, right - 1)
quick_sort(array, right + 1, end)퀵정렬 시간 복잡도
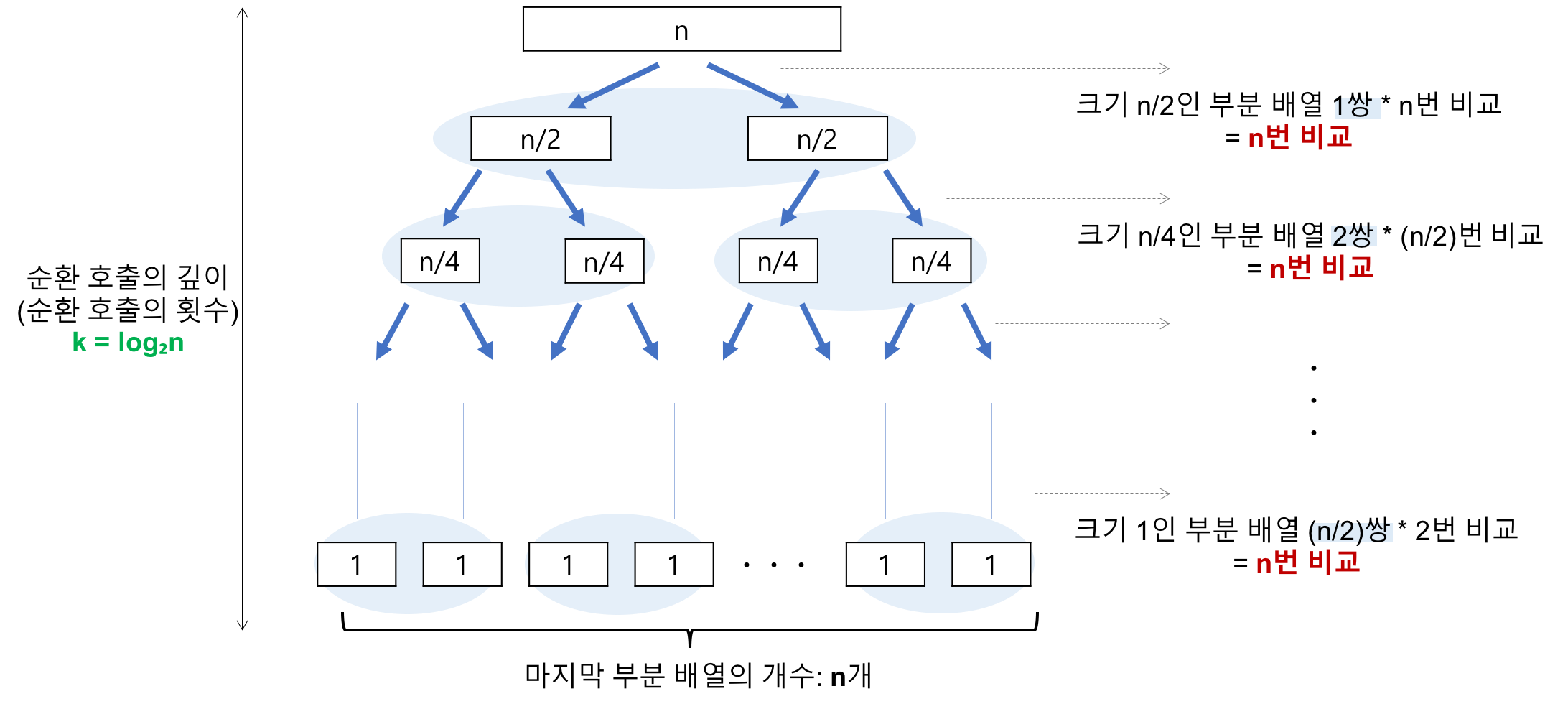
이미지 출처 : Heee's Development Blog(https://gmlwjd9405.github.io/)
- 각 단계에서의 비교 연산 -> n번씩 비교 : O(n)
- 단계의 수 (순환 호출의 깊이) : 병합 정렬과 마찬가지로 O(log₂n)
- 총 O(nlog₂n)
'Algorithm > 개념 정리' 카테고리의 다른 글
| 트리와 그래프 내용 정리 (0) | 2021.12.05 |
|---|---|
| 이분 탐색 정리 (0) | 2021.11.26 |
| 그리디 알고리즘 내용 정리 (0) | 2021.11.23 |
| 분할과 정복 내용정리 (0) | 2021.09.13 |
| 재귀 알고리즘 내용 정리 (0) | 2021.09.06 |

