Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 파이썬
- Kotlin
- BFS
- 백준 온라인 저지
- 정렬
- Level 1
- iOS개발
- UIKit
- 알고리즘 공부
- 파이썬 풀이
- 백준온라인저지
- swift
- 그리디 알고리즘
- 안드로이드 공부
- Python
- 앱개발
- 오토레이아웃
- Android
- ios
- 알고리즘
- 공부
- SwiftUI
- greedy algorithm
- error
- Swift공부
- 프로그래머스
- dfs
- Autolayout
- Algorithm
- Clean Architecture
Archives
- Today
- Total
Tori의 개발 공부
[알고리즘 / Swift] 힙 Heap 본문
Heap 이란?
데이터에서 최댓값 최솟값을 빠르게 찾기 위해 고안된 완전 이진트리로 우선순위 큐를 위해 만들어진 자료구조
- 최대힙(max heap) : 부모노드 ≥ 자식노드
- 최소힙(min heap) : 부모노드 ≤ 자식노드
💡 완전 이진 트리란?
이진트리 = 자식 노드가 최대 두 개인 트리
완전 이진트리 = 마지막 레벨을 제외한 모든 노드가 2개씩 채워져 있으며, 최하단 레벨 또한 좌측부터 채워져있는 노드를 의미한다. 즉 완전 이진트리는 왼쪽부터 자식 노드를 차례로 채운다.
index 성질
heap은 완전 이진 트리 구조이기 때문에 노드 간 인덱스 관계를 나타낼 수 있다.
→ 완전 이진트리는 무조건 왼쪽부터 채워지기 때문에 채워지는 순서가 있음 = index
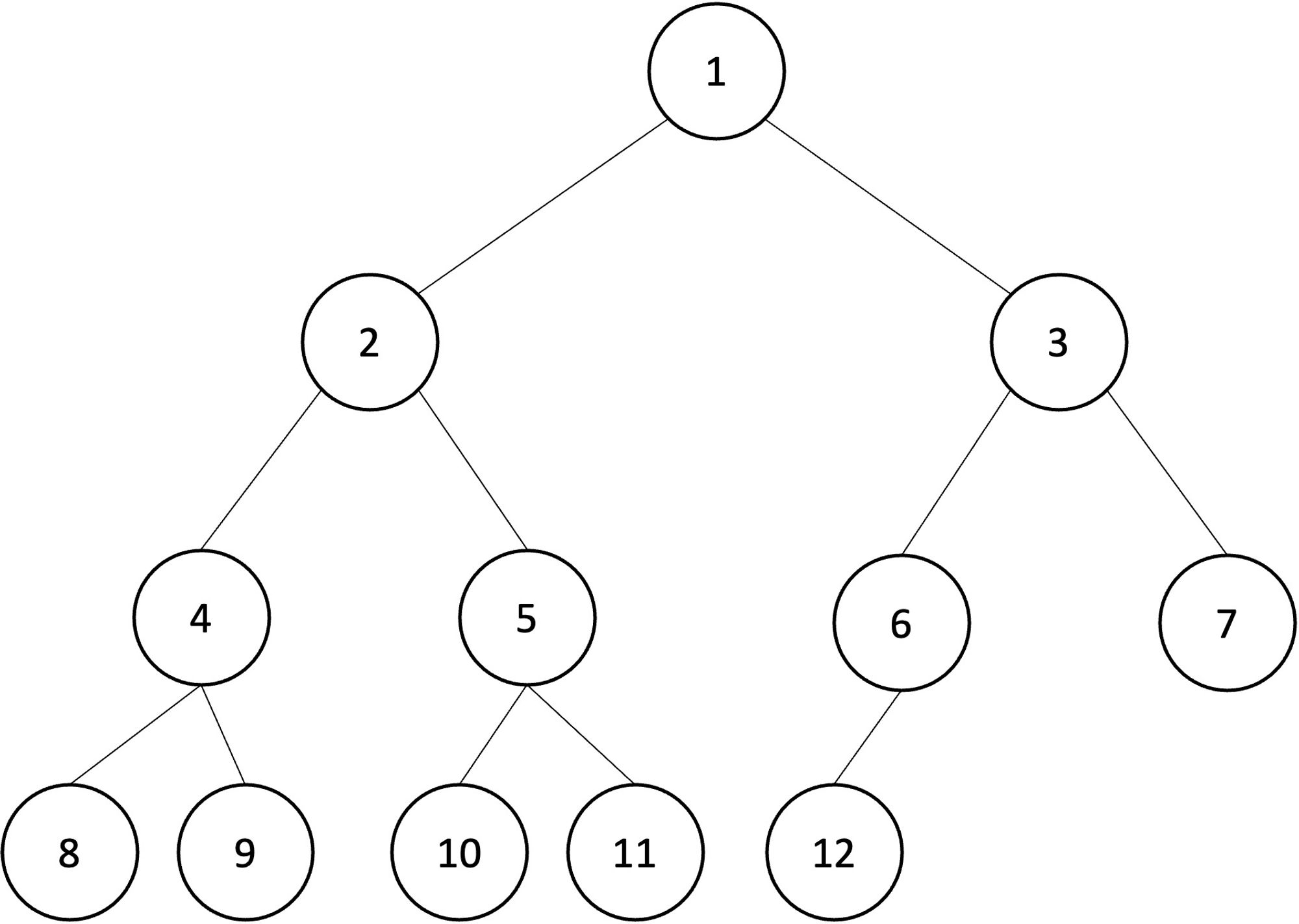
- 부모 노드 index = 자식 노드 index / 2
- 왼쪽 자식 index = 부모 노드 index * 2
- 오른쪽 자식 index = 부모 노드 index * 2 + 1
⇒ 이러한 인덱스 성질을 이용하여 heap을 배열로 구현할 수 있음
Swift로 Heap 구현하기
최대힙을 예시로 heap을 구현해 보았다.
struct Heap<T: Comparable> {
var heap: Array<T> = []
init() {}
init(data: T) {
heap.append(data) // 0번 인덱스 버리기용
heap.append(data)
}
}
기본적인 heap 구조는 다음과 같다. 힙을 나타낼 배열을 초기화해 준다.
이때 처음 초기화 시 데이터를 두 번 넣는 이유는 인덱스를 1부터 시작하기 위해 0번 인덱스에 임의의 값을 넣어준 것이다.
insert(_ data: T)
값을 넣어줄 때는 어떻게 해야 할까?
- 완전 이진트리의 구조에 맞춰 가장 마지막 노드에 새로운 데이터를 삽입한다.
- 부모와 비교하면서 (최대 힙의 경우) 현재 노드가 부모보다 데이터가 클 경우 현재 노드와 부모 노드의 위치를 바꿔준다.
- (최소 힙의 경우) 부모노드 보다 현재 노드가 작다면 위치 변경
- 삽입된 데이터가 힙의 조건을 만족할 때까지 부모와 비교하며 자리를 바꿔준다.
- 최대 힙 : 부모 노드보다 삽입된 노드가 작을 때까지
- 최소 힙 : 부모 노드보다 삽입된 노드가 클 때까지
mutating func insert(_ data: T) {
// 만약 힙이 비어 있다면 1번 값 추가 = init 과 동일
if heap.isEmpty {
heap.append(data) // 0번 인덱스 버리기용
heap.append(data)
return
}
heap.append(data)
func isMove(_ index: Int) -> Bool {
if index <= 1 {
return false
}
let parentIndex = index / 2
return heap[index] >= heap[parentIndex] ? true : false
}
var currentIndex = heap.count - 1
while isMove(currentIndex) {
let parentIndex = currentIndex / 2
heap.swapAt(parentIndex, currentIndex)
currentIndex = parentIndex
}
}
- 기본적으로 struct의 프로퍼티를 변경시키는 함수이기에 mutating 키워드를 사용한다.
- isMove 함수는 매개변수로 받은 인덱스의 값과 부모 인덱스의 값을 비교하여 위치를 바꿀지 여부를 판단하여 Bool 값으로 반환해 준다.
pop()
힙에서 데이터를 꺼내는 상황은 언제일까?
힙의 정의를 다시 살펴보면 데이터에서 최댓값 최솟값을 빠르게 찾기 위해 고안된 완전 이진트리이다.
즉 최댓값 혹은 최솟값을 꺼내주는 것 = 루트 노드를 꺼내는 것
- 루트 노드의 데이터를 삭제한다.
- 가장 마지막 노드를 루트 노드로 이동한다.
- 이동된 노드와 자식 노드들을 비교하며 조건에 맞을 때까지 자식 노드와 위치를 바꿔준다.
- 최대 힙 : 이동된 노드가 자식 노드보다 작다면 위치 변경
- 최소 힙 : 이동된 노드가 자식 노드보다 크다면 위치 변경
mutating func pop() -> T? {
if heap.count <= 1 {
return nil
}
let returnData = heap[1]
heap.swapAt(1, heap.count - 1)
heap.popLast()
func move(_ index: Int) -> downDirection {
let leftIndex = index * 2
let rightIndex = index * 2 + 1
if leftIndex > heap.count - 1 {
// 자식 노드가 없는 경우, 왼쪽 노드부터 채워지므로 왼쪽 노드가 범위를 벗어나면 자식 노드가 없는 경우임
return .stop
}
if rightIndex > heap.count - 1 {
// 왼쪽 자식 노드만 있고 오른쪽 자식 노드는 없는 경우 -> 왼쪽 자식 노드와 비교
return heap[leftIndex] > heap[index] ? .left : .stop
}
if (heap[leftIndex] < heap[index]) && (heap[rightIndex] < heap[index]) {
// 두 자식 요소가 모두 작은 경우 -> 조건 만족 이동 X
return .stop
}
if (heap[leftIndex] > heap[index]) && (heap[rightIndex] > heap[index]) {
// 두 자식 요소가 모두 큰 경우 -> 더 큰 자식노드와 교체
return heap[leftIndex] > heap[rightIndex] ? .left : .right
}
// 위의 모든 경우의 수를 제외하면 두 자식 노드 소 하나만 큰 경우만 남음 -> left가 현재 노드보다 크다면 left만 큰 경우이고 아니라면 right만 큰 경우임
return heap[leftIndex] > heap[index] ? .left : .right
}
var currentIndex = 1
while true {
switch move(currentIndex) {
case .left:
let leftIndex = currentIndex * 2
heap.swapAt(currentIndex, leftIndex)
currentIndex = leftIndex
case .right:
let rightIndex = currentIndex * 2 + 1
heap.swapAt(currentIndex, rightIndex)
currentIndex = rightIndex
case .stop:
return returnData
}
}
}
enum downDirection {
case right
case left
case stop
}
- struct 상단에 다음과 같은 enum 값을 선언해 두었다. 이는 바꿔줄 자식 노드의 위치를 의미하면 stop은 이동하지 않음을 의미한다.
- 따라서 move 함수는 여러 분기문을 통해(주석 설명 참조) 경우의 수를 탐색하여 알맞은 이동방향을 반환해 준다.
'Algorithm > 개념 정리' 카테고리의 다른 글
| 트리와 그래프 내용 정리 (0) | 2021.12.05 |
|---|---|
| 이분 탐색 정리 (0) | 2021.11.26 |
| 그리디 알고리즘 내용 정리 (0) | 2021.11.23 |
| 분할과 정복 내용정리 (0) | 2021.09.13 |
| 재귀 알고리즘 내용 정리 (0) | 2021.09.06 |


